When light and light collide

Title: “Evidence for light-by-light scattering in heavy-ion collisions with the ATLAS detector at the LHC”

Author: ATLAS Collaboration

Reference: doi:10.1038/nphys4208

(Originally published on Particle Bites)

According to classical wave theory, two electromagnetic waves that happen to cross each other in space will not interfere. In fact, this is a crucial feature of the conventional definition of a wave, in contrast to a corpuscle or particle: when two waves meet, they briefly occupy the same space at the same time, each without “knowing” about the other’s existence. Particles, on the other hand, do interact (or scatter) when they get close to each other, and the results of this encounter can be measured.

The mathematical backbone for this idea is the so-called superposition principle. It arises from the fact that the equations describing wave propagation are all linear in the fields and sources, meaning that they don’t occur in squares or cubes of those quantities. When we take two such waves that happen to be nearby, the linearity of the equations implies that we can treat the overall wave as just a linear superposition of two separate waves, traveling in different directions. The equations do not distinguish between the two scenarios.

This story gets more interesting after the insights by Albert Einstein who predicted the quantization of light, and the subsequent formal development of Quantum Electrodynamics in the 1940s by Shin’ichirō Tomonaga, Julian Schwinger and Richard Feynman. In the quantum theory of light, it is no longer “just” a wave, but rather a dual entity that can be treated as both a wave and as a particle called photon.

The new interpretation of light as a particle opens up the possibility that two electromagnetic waves may indeed interact when crossing each other, just as particles would. The mathematical equivalent statement is that the quantum theory of light yields wave equations that are not entirely linear anymore, but instead contain a small non-linear part. The non-linear contributions have to be tiny, otherwise we would already have detected the effects, but nonetheless they are predicted to occur by quantum theory. In this context, it is called light-by-light scattering.

Detection

In 2017, The ATLAS experiment at the LHC observed the first direct evidence of light-by-light scattering, using collisions of relativistic heavy-ions. Since this is such a rare phenomenon, it took us a long time to become directly experimentally sensitive to it.

The experiment is based on so-called Ultra-Peripheral Collisions (UPC) of lead ions (Z=82) at a center-of-mass energy of 5.02 TeV (or 5,000 times the mass of the proton). In UPC collisions, the two oncoming beams are far enough apart that the beam particles are less likely to undergo hard scattering, and instead just “graze” each other. This means that the strong force is not usually involved in such interactions, since its range is tiny and it only has intra-nuclear coverage. Instead, the electromagnetic interaction dominates in UPC events.

The figure below shows how UPCs proceed. The grazing of two lead ions leads to large electromagnetic fields in the space between the ions, and this interaction can be interpreted as an exchange of photons between them, since photons are the mediator of electromagnetism. Then, by also looking for two final-state photons in the ATLAS detector (the ‘X’ on the right in the figure), the light-by-light process, $\gamma \gamma \rightarrow \gamma \gamma$, can be probed ($\gamma$ stands for photons).

In order to isolate this particular process from all the other physics happening at the LHC, a series of increasingly tighter selections (or cuts) is applied to the acquired data. The final cuts are optimized to obtain the maximum possible sensitivity to the light-by-light scattering process. This sensitivity depends on how likely it is to select a candidate signal event, and similarly on how unlikely it is to select a background event. The main background physics that could mimic the signature of light-by-light scattering (two photons in the ATLAS calorimeter on an UPC lead-ion data run) include $\gamma \gamma \rightarrow e^+ e^-$, where the final-state electrons and positrons are misidentified by the detector as photons; central exclusive production (CEP) of photons in $g g \rightarrow \gamma \gamma$ (where $g$ is a gluon); and hadronic fakes from $\pi_0$ production in low-pT dijet events, where $\pi_0$’s (neutral pions) decay to a pair of photons.

The various applied selections begin with a dedicated trigger which selects events with moderate activity in the calorimeter and very little activity elsewhere. This is what is expected in a lead-ion UPC collision, since the ions just escape down the LHC beam pipe and are not detected, leaving the two photons as the only visible products. Then a set of selections is applied to ensure that the recorded activity in the calorimeter is compatible with two photons. These selections rely mostly on the shape of electromagnetic showers deposited on calorimeter crystals, which varies for different types of incident particles.

Finally, a series of extra selections is applied to minimize the number of possible background events, such as vetoing any events containing charged-particle tracks in the ATLAS tracker, which effectively removes $\gamma \gamma \rightarrow  e^+ e^-$ events with electrons and positrons mis-tagged as photons. Note that this also removes some of the real light-by-light signal events (about ~10%), where final-state photons undergo photon conversion after interacting with tracker material, but in this case the trade-off is certainly worth it. Another such selection is the requirement that the transverse momentum of the diphoton system be less than 2 GeV. This removes contributions from other fake-photon backgrounds (such as cosmic-ray muons), because it ensures that the net transverse momentum of the system is small, and thus likely to originate in the ion-ion interaction.

The same exact set of selections is applied to both data and Monte Carlo (MC) simulations of the experiment. The MC simulations yield an estimate of how many background and signal events should be expected in data. The table below shows the results.

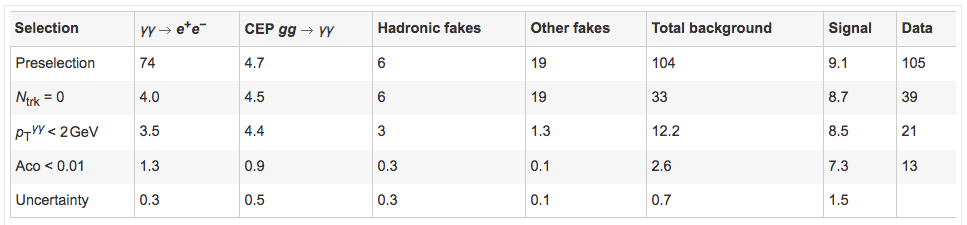
The penultimate row contains the sum of all cuts and a comparison between total number of expected background events (2.6), light-by-light scattering events (7.3), and data (13). The sum of 2.6+7.3=9.9 events certainly seems compatible with the observed data, given the quoted uncertainties in the last row. In fact, it is possible to estimate the significance of this result by asking how likely it would be for the background-only hypothesis (that is, pretending light-by-light scattering doesn’t exist and only including the backgrounds) to yield 13 observed events. This likelihood is tiny, $5\times10^{-6}$, which corresponds to a significance of 4.4 sigma!

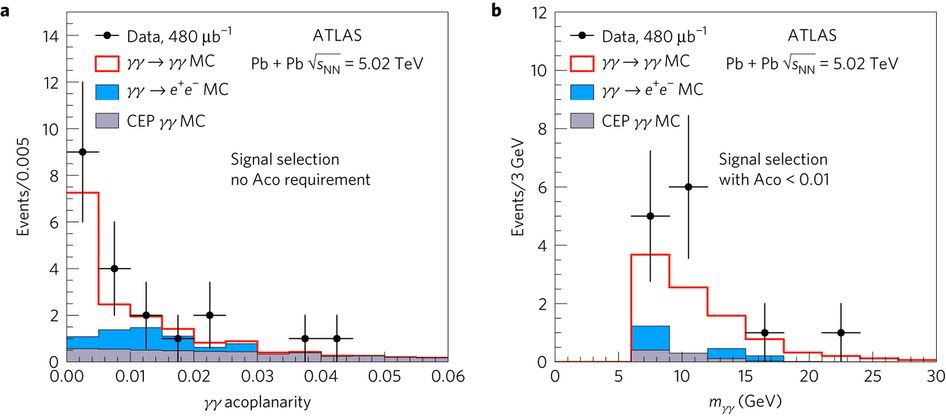
In addition to the number of events, in the figure below the paper also plots the diphoton invariant mass distribution for the 13 observed data events (black points), and for the MC simulations (signal in red and backgrounds in blue and gray). This comparison provides further evidence that we do indeed see light-by-light scattering in the ATLAS data.

Finally, given the observed number of events in data and the expected number of MC background events, it is possible to measure the cross-section of light-by-light scattering (as a reminder, the cross-section of a process measures how likely it is to occur in collisions). The ATLAS collaboration calculates the cross-section of light-by-light scattering with the formula:

$$\sigma_{\text{fid}} = \frac{N_{\text{data}} - N_{\text{bkg}}}{C \times \int L dt}$$

where $N_{\text{data}}$ is the number of observed events in data, $N_{\text{bkg}}$ is the number of background events in MC, $\int L dt$ is the total amount of data collected, and $C$ is a correction factor which translates all of the detector inefficiencies into a single number. You can think of the entire denominator as the “effective” amount of data that was analyzed, and the numerator as the “effective” number of signal events that was seen. The ratio of the two quantities yields the probability of seeing light-by-light scattering in a single collision. The ATLAS collaboration found this value to be $70 \pm 24 ; (\text{statistical}) \pm 17 ;(\text{systematic})$ nb, which agrees with the theorized values of $45 \pm 9$ nb  and $49 \pm 10$ nb within uncertainties.

To conclude, the measurement of light-by-light scattering by ATLAS is an exciting result which offers us a direct glimpse into the stark differences between classical and quantum physics in an accessible (and dare I say) amusing way!